🌊 Tides: Where Gravity Meets the Ocean

Preface

It's February 16th, and tomorrow kicks off my 6th semester. During this break, I had the chance to visit Labuan Bajo for an ocean getaway. While I was there, I noticed something fascinating near the beach – the tides! I could see how the water level near my hotel would change between morning and afternoon. Since I haven't delved into astronomy in a while, I thought this would be the perfect opportunity to dust off my knowledge and write a blog post about tides. I still remember this really cool derivation and visualization of a simple Earth-Moon model that explains how tides work.

What Are Tides

Tides are one of nature's most reliable rhythms, a daily rise and fall of Earth's oceans that has shaped human civilization since ancient times. These periodic movements of water are primarily caused by the gravitational interplay between the Earth, Moon, and Sun, resulting in the regular flooding and ebbing of coastlines worldwide. While most noticeable along beaches and harbors, tidal effects influence everything from marine ecosystems to global weather patterns, making them a crucial component of our planet's environmental systems.

Historical Observations

The story of understanding tides spans diverse cultures and millennia. Ancient civilizations around the world observed and interpreted these rhythmic water movements in different ways. The Yolngu people of northeastern Arnhem Land in Australia developed their own mythological explanation, describing tides as the Moon filling with water and emptying again. Meanwhile, in the Mediterranean region, where tidal effects were less pronounced, various theories emerged - from comparing tides to Earth's breathing to attributing them to underground caverns and whirlpools.

A significant leap in understanding came when Greek scholars began connecting tides to celestial movements. Pytheas of Massilia in 325 BC and later Pliny the Elder noted the relationship between tides and lunar movements, though the exact mechanism remained unclear. The medieval period brought further insights, with scholars like the Venerable Bede demonstrating the connection between twice-daily tides and the Moon's position, as well as the monthly cycle of spring and neap tides. The scientific revolution marked a turning point, with Johannes Kepler correctly suggesting in 1609 that lunar gravitation causes tides. However, not all great minds got it right - Galileo Galilei notably rejected the lunar theory, instead attempting to explain tides through Earth's rotation and revolution around the Sun.

The modern understanding of tides emerged through Isaac Newton's gravitational theory and was later refined by Pierre-Simon Laplace's dynamic theory in 1775. Laplace's work was revolutionary as it accounted for crucial factors like friction, resonance, and the natural periods of ocean basins, finally explaining the complex tidal patterns we observe in our oceans today.

Simple Earth-Moon Model Derivation

A simple model consisting of just the Earth and Moon can provide substantial explanation about the tidal effect. This simple model can be very useful in the Astronomy Science Olympiad. Let's examine a system where only the Earth and Moon exist. We can use the euclidean distance from earth-moon as the $x$ axis, and the $y$ axis perpendicular to it. Let $M$ to be the mass of the Moon, $m$ to be the mass of the object on the Earth's surface, $R$ to be the Earth's radius, $r$ to be the distance between the Earth and the Moon, and $d$ to be the distance between the object and the Moon.

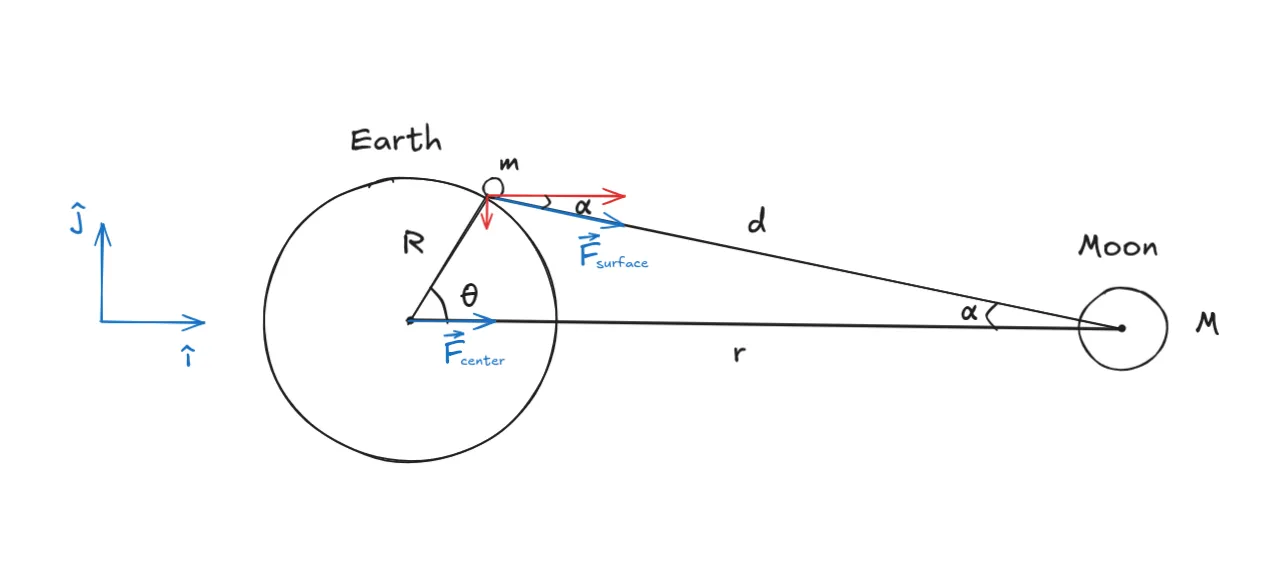
The tidal force is defined as the difference between the force acting on the Earth's surface and the force acting on the Earth's center.

$$\vec{F}_{tide} = \vec{F}_{surface} - \vec{F}_{center}$$

By evaluating the net force in both axes, we get the following expression.

$$\vec{F}_{tide} = \frac{GMm}{d^2}(\cos\alpha\ \hat{\imath} - \sin\alpha\ \hat{\jmath}) - \frac{GMm}{r^2}\hat{\imath}$$

We can also group these forces along each axis.

$$\vec{F}_{tide} = GMm\left[\left(\frac{\cos\alpha}{d^2} - \frac{1}{r^2}\right)\hat{\imath} - \frac{\sin\alpha}{d^2}\hat{\jmath}\right]$$

To simplify the equation, we want to express the tidal force in terms of $G$, $M$, $m$, $R$, $r$, and $\theta$. To do this, we can eliminate $\alpha$ and $d$ using the geometric property of the triangle.

Using the law of sines,

$$\frac{\sin\alpha}{R} = \frac{\sin\theta}{d}$$

$$\sin\alpha = \frac{R}{d}\sin\theta$$

Using the law of cosines,

$$d = (r^2 + R^2 - 2Rr\cos\theta)^{\frac{1}{2}}$$

And examining the base of the triangle,

$$r = R\cos\theta + d\cos\alpha$$

$$\cos\alpha = \frac{r - R\cos\theta}{d}$$

Substitute those equations into the tidal force equation.

$$\vec{F}_{tide} = GMm\left[\left(\frac{r - R\cos\theta}{d^3} - \frac{1}{r^2}\right)\hat{\imath} - \frac{R\sin\theta}{d^3}\hat{\jmath}\right]$$

$$\vec{F}_{tide} = GMm\left[\left(\frac{r - R\cos\theta}{(r^2 + R^2 - 2Rr\cos\theta)^{\frac{3}{2}}} - \frac{1}{r^2}\right)\hat{\imath} - \frac{R\sin\theta}{(r^2 + R^2 - 2Rr\cos\theta)^{\frac{3}{2}}}\hat{\jmath}\right]$$

$$\vec{F}_{tide} = \frac{GMm}{r^2}\left[\left(\frac{1-\frac{R}{r}\cos\theta}{\left(1 + \frac{R^2}{r^2} - \frac{2R}{r}\cos\theta\right)^{\frac{3}{2}}} - 1\right)\hat{\imath} - \frac{\frac{R}{r}\sin\theta}{\left(1 + \frac{R^2}{r^2} - \frac{2R}{r}\cos\theta\right)^{\frac{3}{2}}}\hat{\jmath}\right]$$

Note that $R << r$. We can ignore the second-degree factor $(\frac{R^2}{r^2} \approx 0)$ and also apply the negative exponent rule.

$$\vec{F}_{tide} \approx \frac{GMm}{r^2}\left[\left(\left(1-\frac{R}{r}\cos\theta\right)\left(1-\frac{2R}{r}\cos\theta\right)^{-\frac{3}{2}} - 1\right)\hat{\imath} - \frac{R}{r}\sin\theta\left(1-\frac{2R}{r}\cos\theta\right)^{-\frac{3}{2}}\hat{\jmath}\right]$$

Apply binomial approximation $(1+x)^n \approx nx$ for $|x| << 1$ .

$$\vec{F}_{tide} \approx \frac{GMm}{r^2}\left[\left(\left(1-\frac{R}{r}\cos\theta\right)\left(1+\frac{3R}{r}\cos\theta\right) - 1\right)\hat{\imath} - \frac{R}{r}\sin\theta\left(1+\frac{3R}{r}\cos\theta\right)\hat{\jmath}\right]$$

$$\vec{F}_{tide} \approx \frac{GMm}{r^2}\left[\left(\frac{2R}{r}\cos\theta + \frac{3R^2}{r^2}\cos\theta\right)\hat{\imath} - \left(\frac{R}{r}\sin\theta + \frac{3R^2}{r^2}\sin\theta\cos\theta\right)\hat{\jmath}\right]$$

If we ignore the second-degree factor again, we can obtain

$$\vec{F}_{tide} \approx \frac{GMm}{r^2}\left[\left(\frac{2R}{r}\cos\theta\right)\hat{\imath} - \left(\frac{R}{r}\sin\theta\right)\hat{\jmath}\right]$$

$$\boxed{ \vec{F}_{tide} \approx \frac{GMmR}{r^3}(2\cos\theta\ \hat{\imath} - \sin\theta\ \hat{\jmath}) }$$

Note that the final result is in vector form (not just magnitude), meaning you can see both the magnitude and direction of the vector.

What Does The Equation Tell?

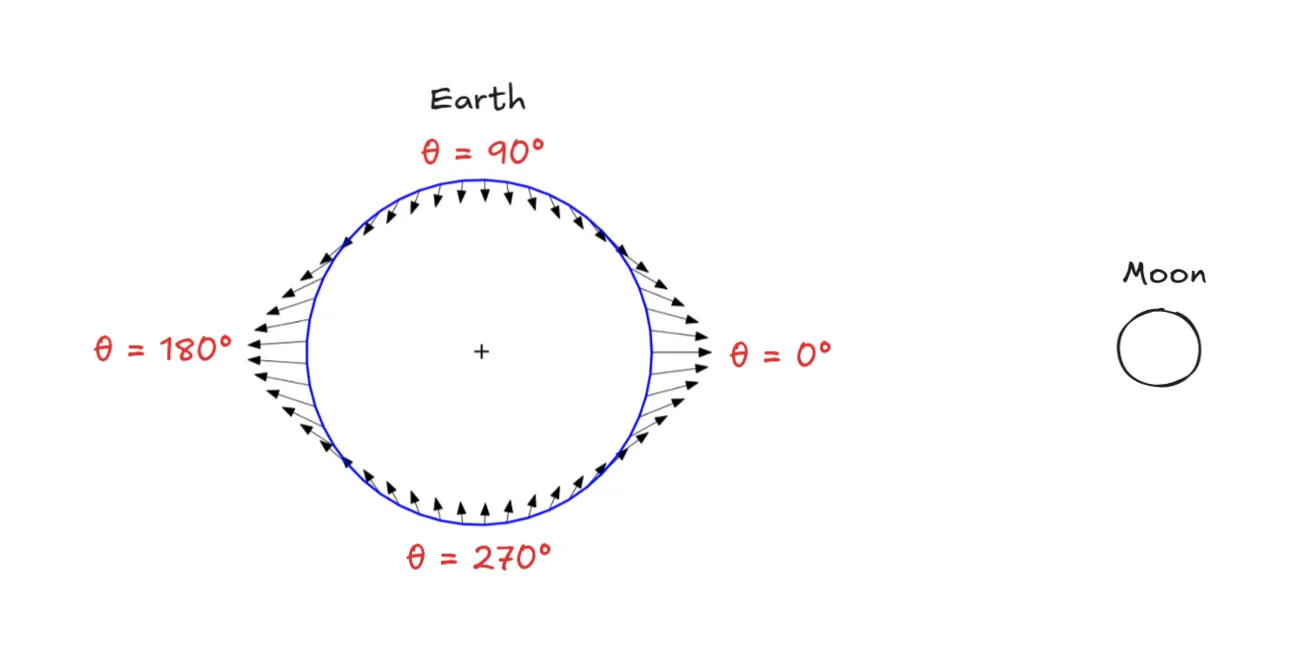
Based on the equations, we can see that the tidal force reaches a maximum value when $\theta = 0 \degree$ (when the Moon is directly overhead) or $\theta = 180 \degree$ (when the Moon is directly below). In both cases, the tidal force is directed outward from the Earth, causing the tide/seawater to rise. The value of the tidal force at these points is

$$\boxed{ |\vec{F}_{tide}| \approx \frac{2GMmR}{r^3} }$$

Additionally, based on the equations, we can see that the tidal force reaches a minimum value when $\theta = 90 \degree$ or $\theta = 270 \degree$ (when the Moon is near the horizon). In both cases, the tidal force is directed inward toward the Earth, causing the tide/seawater to fall. The value of the tidal forces at these points is

$$\boxed{ |\vec{F}_{tide}| \approx \frac{GMmR}{r^3} }$$

Other Factors

While the Earth-Moon model provides a fundamental understanding of tidal forces, real-world tides are significantly more complex due to several additional factors. The Sun, despite being much farther away than the Moon, plays a considerable role in tidal patterns through its own gravitational influence. When the Sun and Moon align (during new and full moons), their combined gravitational forces create stronger "spring tides." Conversely, when they are at right angles to Earth (during quarter moons), we experience weaker "neap tides."

Local geography and topography also dramatically influence tidal patterns. The shape of coastlines, depth of ocean basins, and presence of continental shelves can amplify or diminish tidal effects. For example, the Bay of Fundy in Canada experiences extreme tidal ranges (up to 16 meters) due to its funnel-shaped bay and resonant forcing effects. Similarly, narrow channels, bays, and estuaries can create unique tidal phenomena like tidal bores - waves that travel upstream against river currents.

Earth's rotation introduces additional complexity through the Coriolis effect, which influences ocean currents and tidal patterns. This effect, combined with the presence of continents, creates amphidromic points - locations where tidal range is nearly zero, around which tidal bulges appear to rotate. The Earth's irregular ocean floor topography, varying water depths, and the presence of large-scale ocean currents also modify tidal patterns from their theoretical predictions.

Atmospheric conditions can further modify tidal heights. Strong winds and variations in atmospheric pressure can either enhance or reduce tidal ranges, a phenomenon known as storm surge when combined with severe weather events. These factors make accurate tidal prediction a complex task requiring sophisticated mathematical models that account for multiple variables beyond simple gravitational interactions.

References

Wikipedia Contributor. (14 February 2025). Tide. Wikipedia, The Free Encyclopedia. Source .

Wikipedia Contributor. (3 January 2025). Theory of tides. Wikipedia, The Free Encyclopedia. Source .